SGPS REAL-TIME ORBIT DETERMINATION

On-orbit, orbit determination (OD) is invariably performed in real-time or near real-time in the GPS receiver. Therefore to perform real-time orbit determination with GPS, it is most efficient to incorporate the OD software into the receiver. This involves absolute position determination with a GPS receiver.

Benefits of GPS:

The ability to determine space vehicle orbits quickly, with comparable or superior accuracies than can be achieved via ground station tracking.

Methodology:

Absolute position determinations can be performed in real-time with GPS receivers that have software capability to track GPS signals from fast moving space platforms. The range of the received Doppler frequency signals are about 100 kHz in a LEO spacecraft, as compared to a receiver on the ground for which this width is approximately one tenth as wide. By utilising its pseudorange and carrier phase observations, the receiver can determine its position and velocity in real-time as does a receiver operating on the earth's surface. This is its navigation solution or state vector. It must be observed that the accuracies of these solutions are difficult to assess due to the lack of known position information. Software code in the receiver or in another system on-board the satellite must convert the receiver-derived state vector to an orbit determination. The simplest case is an osculating ellipse for a single epoch. A more comprehensive orbit determination would involve the use of a satellite force model with the state vectors and a Kalman filter.

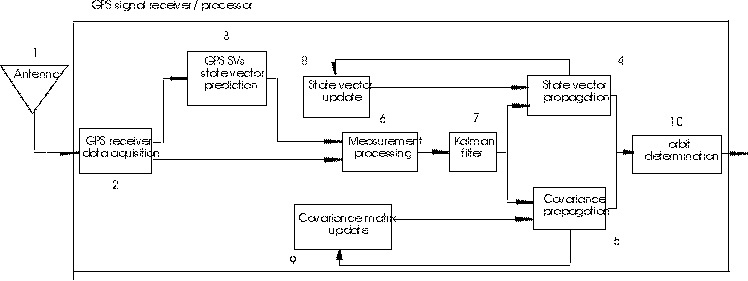
The above figure illustrates a generic real-time, onboard, orbit determination architecture flowchart design from research by Potti et al. [1995].

GPS signals are received at the antenna (1) and are tracked in the data acquisition section (2). If single frequency data are being collected, ionosphere corrections are required if ionospheric propagation delay of the signals is to be removed.

The state vector of the GPS satellites is predicted (3) from the GPS navigation message obtained by the data acquisition section (2) for the design matrix computation. The state vector and its covariance matrix for orbit determination must be initialised from input parameters.

The propagation of the state vector (4) and the state vector error covariance matrix (5) are performed by analytical and/or numeric integration. A change in the GPS satellite constellation being tracked would require a re-initialisation of the state vector elements pertaining to the specific satellite(s) involved. An orbit dynamics model is incorporated at this stage.

The measurement processing section (6) utilises an extended Kalman filter (7) (EKF), due to the non-linear formulation, to predict the states between two updates. These predicted states are differenced from the measured observables to determine the measurement residuals. The observation matrix is determined.

An EKF is used to update the state vector (8) and the covariance matrix (9).

Finally from the updated state comes the orbit determination (10).

Mission examples:

Real-time, on-orbit, OD results are found sparingly in the literature. Therefore, navigation solutions, post-processed and simulated results are also included in this section.

- The SFU mission produced a real-time, on-orbit OD solution accuracy of 200 m +- <200 m.

- The EUVE mission produced a solution accuracy of 10 to 15 m in a post-processed simulated real-time scenario.

- The PoSat-1 mission produced a solution accuracy of 1.5 km in which the receiver was turned on for only one orbit per day.

- The DARPASAT mission produced a solution accuracy of 350 m. The navigation solution was however compared to radar range vectors.

- The GPS/MET mission in one test produced a receiver navigation solution accuracy of 46 m.

- The Wake Shield Facility-02 mission produced a solution accuracy of 62.6 m with a post-processed least squares fit of an orbit to a navigation solution.

- The SSTI Lewis mission proposes real-time total one sigma position and velocity accuracy of 20 m and 0.03 m/s, repsectively.

Related Internet Sites:

GSFC GPS-Based Onboard Navigation Systems page

References:

Due to the rapid developments in the field of spaceborne GPS and the aerospace industry in general, any comments, information or corrections pertaining to information on this site are welcome and encouraged.