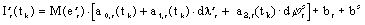The Effect of Shell Height on High Precision Ionospheric Modelling Using GPS

A. Komjathy and R.B. Langley

Both at: Geodetic Research Laboratory, Department of Geodesy and Geomatics Engineering

University of New Brunswick, P.O. Box 4400, Fredericton, N.B. E3B 5A3 Canada

Phone: 1-506-453-4698, Fax: 1-506-453-4943, email: lang@unb.ca

ABSTRACT

The dispersive nature of the ionosphere makes it possible to measure its total electron content (TEC) using dual-frequency Navstar Global Positioning System (GPS) observations collected by permanent networks of GPS receivers. One such network is that of the International GPS Service for Geodynamics (IGS). UNB has participated in an ionospheric experiment along with other ionospheric research groups under the auspices of the IGS and European Space Agency's European Space Operations Centre (ESA/ESOC). A 5 week long period of dual-frequency GPS measurements collected by IGS stations was designated as a test data set for the different research groups to analyse and produce TEC values and satellite-receiver differential delays. One of the primary goals of the experiment was to analyse the effect of geomagnetic disturbances on the ionospheric products. We have used dual-frequency GPS pseudorange and carrier phase observations from six European stations in the IGS network to derive regional TEC values and satellite-receiver differential delays.

In an earlier study we concluded that after processing data from 6 European stations collected over a 7 day period (the first 7 days of the ionospheric experiment organized by ESA/ESOC), we were able to follow highly varying ionospheric conditions associated with geomagnetic disturbances. We investigated the effect of using different elevation cutoff angles and ionospheric shell heights on the TEC estimates and satellite-receiver differential delays. These results pertaining to GPS week 823 have been presented earlier [Komjathy and Langley, 1996]. In our current research, we used 21 days' worth of data in a continuation of the study mentioned earlier with a more rigorous approach for ionospheric shell height determination which has been derived from the International Reference Ionosphere 1990 (IRI90) [Bilitza, 1990]. We looked at the effect of using ionospheric shell heights fixed at a commonly used altitude (400 km) on the TEC and differential delay estimates. We found differences in the differential delays between the two approaches of up to the 0.3 ns (approximately 1 total electron content unit - TECU) level and differences in the TEC estimates up to the 1 TECU ( approximately 0.16 m delay on L1) level. We also compared our differential delay estimates with those obtained by other research groups participating in the experiment. We found agreement in the differential delays between three analysis centers at the 1 ns level.

INTRODUCTION

The electromagnetic signals from the GPS satellites must travel through the earth's ionosphere on their way to GPS receivers on or near the earth's surface. Whereas these effects may be considered a nuisance by most GPS users, they will provide the ionospheric community with an opportunity to use GPS as a tool to better understand the plasma surrounding the earth. Dual-frequency GPS observations can be used to eliminate almost all of the ionosphere's effect. To correct data from a single-frequency GPS receiver for the ionospheric effect, it is possible to use empirical models. We are conducting an on-going study to assess the accuracy and efficacy of such models.

We decided to include the new IRI90 model [Bilitza, 1990] in our ionospheric research after Newby [1992] investigated the International Reference Ionosphere 1986 (IRI86) model's performance. Earlier we used Faraday rotation data as "ground-truth" with which we compared the vertical ionospheric range error corrections predicted by the Broadcast model of the GPS navigation message [Klobuchar, 1986] and the IRI90 model. For low solar activity, mid-latitude conditions we concluded that based on the comparison between the Broadcast and IRI90 models, both for day-time and night-time periods, the IRI90 model appeared to be more accurate than the Broadcast model [Komjathy et al., 1995a ; 1995b]. Since data from the GOES geostationary satellites that would provide the Faraday rotation measurements for use as "ground-truth" is no longer readily available, we have decided to use dual-frequency pseudorange and carrier phase GPS measurements to infer ionospheric TEC.

Early studies used single station observations to estimate the line-of-sight pseudo-TEC which is the sum of the satellite-receiver differential delays and the actual line-of-sight TEC (e.g., Lanyi and Roth [1988], Coco et al. [1991]). Recently the ionospheric community started applying multi-site fitting techniques to produce global and/or regional ionospheric maps with more accurate TEC and differential delay estimates. These ionospheric maps and differential delays are becoming freely accessible on the Internet. As an ionospheric observable, most research groups use a "phase-levelling" technique in which the integer ambiguity afflicted differences of the L1 and L2 (L1-L2) carrier phase measurements are adjusted by a constant value determined for each phase-connected arc of data using precise pseudorange measurements. This technique is widely used to estimate ionospheric model parameters as well as satellite-receiver differential delays (see, e.g., Gao et al. [1994], Sardon et al. [1994], Wilson and Mannucci [1994], and Runge et al. [1995]). It is also feasible to use double-differenced L1-L2 carrier-phase observations to estimate global or regional ionospheric models [Schaer et al. 1995]. The advantage of this latter technique is that by using the double-differenced ionospheric observable, one does not have to estimate the satellite-receiver differential delays as they are differenced away although some of the resolution of the ionospheric signal is eliminated during the process. A technique used by Bishop et al. [1995] infers TEC and satellite-receiver differential delays by requiring maximum agreement between ionospheric measurements when the observed paths of two satellites cross.

ESTIMATION STRATEGY

The estimation strategy we used is described in Komjathy and Langley [1996] in detail. In this section, we will briefly summarize the basic principles of our technique to help explain the recent improvements we made to the algorithm. We model the ionospheric measurements from a GPS receiver with the commonly used single-layer ionospheric model using the observation equation:

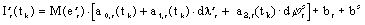Click on equation for explanation of symbols (9k)

The three stochastic parameters in the above equation are estimated for each station using a Kalman filter approach. The prediction and update equations for the state estimation are described by e.g., Schwarz [1987], Coster et al. [1992] and van der Wal [1995]. Due to the highly varying ionospheric conditions during the observation window processed, we allowed the model to follow a relatively high 1 TECU per 2 minutes change in the total electron content which resulted in the process noise variance rate of change being 0.008 TECU*TECU/ second characterizing the uncertainties of the dynamic ionospheric model. For the variance of the measurement noise, we used 1 TECU*TECU the assumed uniform uncertainty in the observations.

We estimated the combined satellite-receiver differential delays for station Madrid. In a network solution, additional differential delay parameters for the rest of the stations have to be estimated based on the fact that the other receivers have different differential delays. Therefore, for each station other than station Madrid, an additional differential delay parameter was estimated which is the difference between the receiver differential delay between a station in the network and station Madrid. This technique is described by e.g., Sardon et al. [1994].

We chose a solar-geomagnetic reference frame based on sun-fixed longitude and geomagnetic latitude since the main reason for the ionosphere's existence is the interaction of ionizing radiation (principally from solar ultraviolet and x-ray emissions) with the earth's atmosphere and magnetic field [Langley, 1996]. Furthermore, the ionosphere varies much more slowly in sun-fixed reference frame than in an earth-fixed one. The use of such a reference frame results in more accurate ionospheric delay estimates when using Kalman-filter updating [Mannucci et al.,1995].

A parameter that affects the TEC estimation is the assumed height of the ionospheric shell which plays a role in computing the coordinates of the subionospheric points. It is also an input parameter of the mapping function (see equation). At this stage we use a simple secant mapping function. Later on, we plan on looking at other mapping functions that would reduce mapping function errors for low elevation angle satellites. The single-layer ionospheric model assumes that the vertical TEC can be approximated by a thin spherical shell which is located at a specified height above the earth's surface. This altitude is often assumed to correspond to the maximum electron density of the ionosphere. Furthermore, it is usually assumed that the ionospheric shell height has no temporal or geographical variation and therefore it is set to a constant value regardless of the time or location of interest. In Komjathy and Langley [1996], we looked at the effect of different fixed ionospheric shell heights of 300, 350, and 400 km and also included variable heights computed by the IRI90 model using F2 layer peak heights. We found that at the 2 TECU level, the ionospheric estimates using these specified heights agree depending on geographic location and time of the day. We also found that using different elevation cutoff angles (15deg, 20deg, and 25deg) had an impact on TEC estimates at the 2 TECU level. These results should be considered only valid for the low solar activity conditions under which the estimates were made.

After the promising results of using the IRI90 model for ionospheric shell height determination, we decided to carry on with this investigation. In our current study, we use the IRI90 model to compute even more accurate ionospheric shell heights by integrating the predicted electron densities through the six subregions of the IRI90 profile. Ionospheric shell height predictions were obtained upon reaching 50 percent of the predicted total electron content during the numerical integration procedure using a step size of 1 km. We computed the predicted total electron content up to an altitude of 1000 km (see Figure 1), consequently, plasmaspheric electron content has not been considered at this stage but its effect should be less than about 50 percent of the night-time total electron content near sunspot minimum [Davies, 1990]. The omission of the plasmaspheric electron content has an effect primarily on the night-time TEC predictions at the 2 TECU level. We believe that this method provides an even more rigorous approach compared to what has been described in Komjathy and Langley [1996]. Note in Figure 1 that the predicted ionospheric shell height is always slightly above the height of the F2 layer peak electron density since the topside region of the ionosphere contains more electrons than the bottomside. The predicted ionospheric shell heights are used as input into our software for estimating TEC maps as well as satellite-receiver differential delays.

THE DATA SET

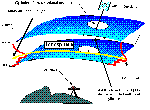
Along with several other research groups, we participated in an experiment to assess the capabilities of GPS data to provide TEC values. Organized under the auspices of the International GPS Service for Geodynamics (IGS) and the Orbit Attitude Division of the European Space Agency's European Space Operations Centre (ESA/ESOC), the experiment involves the processing and analysis of a 5 week long data set of dual-frequency GPS data from the stations of the IGS network (GPS weeks 823 through 827). We have analysed the GPS data sets from 6 of the European IGS stations. The stations are Madrid, Grasse, Matera, Brussels, Wettzell, and Onsala and are identified on the map in Figure 2. The differences in geomagnetic latitudes of stations Madrid, Grasse, and Matera are less then 5 degrees, and 3.3 degrees in the case of stations Brussels and Wettzell. Therefore, we can identify three distinct latitude regions in our test network (1. Madrid, Grasse, Matera; 2. Brussels, Wettzell; 3. Onsala). All 6 stations use Allen Osborne Associates TurboRogue receivers.

We processed 21 days' worth of data from the 6 stations spanning the time period 15 October to 4 November 1995 (GPS weeks 823, 824, and 825) during which a geomagnetic disturbance occurred [NGDC, 1995]. The planetary equivalent amplitude of magnetic activity ap suggests that the magnetic disturbance started on 18 October 1995 (day of year 291) and lasted for about 6 days until 23 October 1995 (day 296). The peak (ap = 111) occurred on 19 October 1995. The magnetic disturbance on day 292 affected the diurnal variation of the total electron content. The effect of this disturbance on our TEC estimates has been discussed previously in Komjathy and Langley [1996]. In that study we found that on day 292, at stations Madrid, Grasse and Matera, the diurnal peak of TEC values increased considerably compared to diurnal peaks for the previous days. On the other hand, for stations Brussels, Wettzell and Onsala, the GPS-derived TEC estimates show diurnal peaks with smaller size than the ones on the previous days. Also, even though the magnetic disturbance started during European night-time, it only caused a TEC increase (stations Madrid, Grasse, Matera) and decrease (Brussels, Wettzell) on the following day around noon (day 292). The fact that we detected at some stations a TEC increase and at others a TEC decrease may suggest that the magnetic disturbance was moving equatorward which is a well known feature of such disturbances [Davies, 1990].

Click on figure for larger image (15k)

Figure 1. Illustration of ionospheric shell height determination.

Figure 2. Locations of IGS stations used for data analysis.

RESULTS AND DISCUSSION

We used the PhasEdit version 2.0 automatic data editing program to detect bad points and cycle slips, repair cycle slips and adjust phase ambiguities using the undifferenced data. The program takes advantage of the high precision dual-frequency pseudorange measurements to adjust L1 and L2 phases by an integer number of cycles to agree with the pseudorange measurements [Freymueller, 1995]. Subsequently, a modified version of the University of New Brunswick's DIfferential POsitioning Program (DIPOP) package was used to estimate ionospheric parameters and satellite-receiver differential delays using a Kalman filter algorithm.

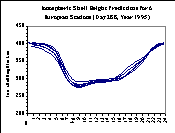
For our investigation, we used the IRI90-derived ionospheric shell height predictions as input into our DIPOP-based processor. As a first step, we computed the IRI90 predicted total electron content by integrating the predicted electron densities along the IRI90 profile. A simplified version of the profile can be seen in Figure 3 (for an explanation of the symbols, see Hakegard [1995] or Bilitza [1990]). Secondly, we used these TEC predictions to integrate the electron densities along the profile again. This time, the goal was to determine the height at which 50 percent of the total electron content was reached. We did this for all six stations we used for data processing for the 21 days under investigation. As an example, we have plotted the predicted ionospheric shell heights for day 288 in Figure 4. We can clearly see a diurnal variation of the IRI90-derived ionospheric shell height. The shell height seems to peak at night-time values of about 400 km and goes down to day-time values typically at the 300 km level. Diurnal curves were plotted for all 6 stations for day 288. There are noticeable differences from station to station even under the current low solar activity conditions. The spatial variation of the ionospheric shell height in our regional network for GPS weeks 823 to 825 was between 10 and 30 km depending on the time of the day.

Click on figure for larger image (3k)

Figure 3. IRI90 profile (after Hakegard, [1995]).

Click on figure for larger image (4k)

Figure 4. The diurnal variation of the ionospheric shell height.

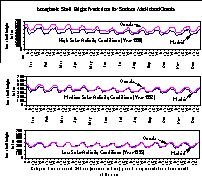
For a better understanding of the magnitude range of varying ionospheric shell height, we computed the predicted ionospheric shell heights for high (year 1990), medium (year 1992) and low (year 1995) solar activity conditions. In Figure 5, we plotted the diurnal curves for the two stations that are furthest apart in our network: stations Madrid and Onsala. Each diurnal curve represents the conditions for the 15th day of one month of the year displaying not only the diurnal variation but also the seasonal variation of the ionospheric shell height. Note that the x axis is a category time axis on which 12 diurnal curves have been plotted one after the other each representing a "typical day" of a month. The "typical day" was arbitrarily chosen to be the 15th day of the month for illustration purposes. A small discontinuity is visible between some of the curves at 24 hours reflecting month-to-month variations. During high solar activity conditions, the peak to peak variation of the diurnal curve is between 400 and 600 km, depending on season and geographic location of the station. During medium solar activity conditions, the variation is between 300 and 500 km. For low solar activity conditions this variation is between 300 and 400 km. As solar activity decreases, the dependency on geographic location, at least for our two European stations, becomes less significant. For high solar activity conditions, station Onsala (furthest north in the network) had the highest ionospheric shell heights. Also, during winter months the separation between shell heights predicted for stations Onsala and Madrid seems to be larger than for the rest of the year. For high solar activity conditions, the average ionospheric shell height is around 466 km; for medium solar activity conditions, 385 km; for low solar activity conditions, 335 km. It seems that the diurnal, seasonal, solar-cycle and spatial variations of the ionospheric shell heights are associated with the temporal and spatial variation of the F2 layer peak electron density.

Click on figure for larger image (12k)

Figure 5. Ionospheric shell height predictions using the IRI90 model.

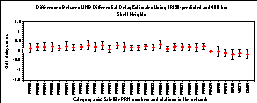
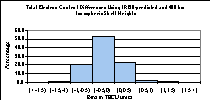
Using varying ionospheric shell heights as input into our model produces TEC and satellite-receiver differential delay estimates that are somewhat different from those obtained using a fixed ionospheric shell height. To determine the magnitude of the differences, we produced a set of TEC and differential delay estimates using both a commonly adopted fixed ionospheric shell height (400 km) and varying ionospheric shell heights predicted by the IRI90 model as described earlier. The entire 21 days' worth of data was used for this investigation. We differenced the means (over 21 days) of the differential delay estimates for each satellite and station using the varying IRI90-predicted and 400 km ionospheric shell heights. The differences in differential delays can be seen in Figure 6. The differences are less than 0.3 ns with a mean of 0.14 ns and mean standard deviation of 0.13 ns. In Figure 6, the error bars represent the mean standard deviation of the UNB differential delay estimates. We also produced hourly TEC maps at a 1 degree by 1 degree grid spacing for the region displayed in Figure 2. We produced the TEC maps by evaluating at each grid node our expression for the spatial linear approximation of TEC described by the three parameters estimated for each IGS station. For evaluating the model at each grid node, we used the three estimated parameters from the nearest IGS station. In the future, we will modify this approach with an appropriate multi-station weighting scheme. We used both the varying and 400 km ionospheric shell heights to compute different sets of ionospheric maps. We differenced the corresponding TEC values at each grid node that were computed for each hour of the 21 days under investigation. The differences are plotted in Figure 7. The histogram is based on 640,584 ((31 by 41 grid) times (24 hours ) times (21 days)) TEC estimates. 53 percent of the differences fall into a bin that can be characterized with a lower boundary of -0.5 TECU and upper boundary of 0 TECU. The mean of the differences is -0.34 TECU and its associated standard deviation is 0.58 TECU. Note that the TEC differences were formed by subtracting TEC values using a 400 km shell height from those using the IRI90-derived shell height TEC values.

Click on figure for larger image (6k)

Figure 6. Comparison of satellite-receiver differential delay estimates between using IRI90-derived and 400 km ionospheric shell heights.

Click on figure for larger image (4k)

Figure 7. Comparison of TEC estimates between using IRI90-derived and 400 km ionospheric shell heights.

We conclude from this investigation that taking the temporal and spatial variation of the ionospheric shell height into account has an effect on the TEC estimates of up to 1 TECU, and 0.3 ns in the case of the differential delay estimates. These values will likely only hold for mid-latitude conditions at low solar activity levels. As we have seen earlier in Figure 5, during higher solar activity times, we can expect these differences to increase. The 1 TECU level differences are fairly small and may be within the error bars of the TEC estimates. Therefore, we decided not to compare our TEC estimates (maps) with those obtained by other research groups to try to determine the effects of using different values for the ionospheric shell height. Furthermore, the differences between ionospheric modelling methods used by different groups would make it difficult to draw conclusions on the specific effect of their selected ionospheric shell heights.

Instead, we computed the means and the standard deviations of our daily differential delays for all 21 days. We also obtained a set of differential delay estimates computed by two of the other participating members of the ionospheric experiment, namely, the Deutsche Forschungsanstalt fur Luft und Raumfahrt (DLR) Fernerkundungsstation, Neustrelitz, Germany and the European Space Agency's European Space Operation Centre (ESA/ESOC), Darmstadt, Germany. After computing the means and standard deviations of the differential delays obtained from DLR and ESOC for all 21 days, we computed the differences of the corresponding means. The differences among the 3 analysis centers' results are displayed in Figure 8.

Click on figure for larger image (9k)

Figure 8. Comparison of differential delay differences between processing centers.

The differences were formed as UNB minus DLR and UNB minus ESOC using both our IRI90-derived shell height results (upper panel) and our results using the 400 km shell height (lower panel). Note in Figure 8 that satellites PRN12 and PRN28 are not used by DLR and stations Grasse and Brussels are not processed by ESOC. The associated standard deviations of the differential delays about the means of the two other processing centers were also plotted. The standard deviations of the means of the UNB differential delays were plotted earlier in Figure 6 and have not been considered in computing the error bars in Figure 8. The differences of the differential delay estimates are at the 1 ns level for both shell height models (upper and lower panel). It is interesting to see that there is a clear bias between the DLR and ESOC satellite differential delays. A part of the bias can be explained by the fact that the ESOC algorithm uses 350 km for the ionospheric shell height whereas the DRL algorithm uses 400 km. As our investigation indicated in Figure 6, a 0.14 ns level bias can be expected between the differential delay differences using the IRI90-derived differential delays and the ones obtained using 400 km. However, a 1 ns level difference indicates that there are effects coming from other differences in the algorithms used by the processing centers. The fact that the UNB-ESOC differences do not seem to show a consistent bias might be explained by the fact that the mean of the IRI90-predicted diurnal variation of the ionospheric shell height is around 335 km under low solar activity conditions which is close to the 350 km height used by ESOC.

One of the potential error sources that may contribute significantly to the UNB error budget is the mapping function error. Since we use a simple secant mapping function at this stage, this could introduce unwanted errors at low elevation angles (say between 20 and 30 degrees). Throughout our processing, we used a 20 degree elevation cutoff angle. The very ability to do ionospheric modelling is based on the possibility of separating estimates of TEC from differential delays by using the elevation angle dependence of the TEC variation. Should this separation suffer from mapping function errors, a bias could be introduced into both the TEC and differential delay estimates.

It seems that using pre-defined values for ionospheric shell height has a scaling effect on the differential delay estimates. The results presented in Komjathy and Langley [1996] were also indicative of this. The lower the ionospheric shell height is set (arbitrarily or otherwise) from the "true" value, the higher the estimated differential delays will be. Furthermore, this effect seems to have an opposite sign in the case of the TEC estimates: The lower the ionospheric shell height is set from the "true" value, the lower TEC estimates can be expected. Using pre-defined fixed values for ionospheric shell height may lead to errors both in the satellite-receiver differential delays and the TEC estimates. This conclusion seems to be supported by the maximum 0.3 ns error in differential delay differences we found which corresponds to about 1 TECU. This also corresponds to the maximum TEC differences that were found to be at the 1 TECU level (see Figure 7). Using 400 km as a fixed ionospheric shell height during low solar activity conditions overestimates the day-time TEC by up to 1 TECU assuming that the IRI90-derived ionospheric shell height predictions are free of error. In the case of the satellite-receiver differential delays, using a fixed 400 km ionospheric shell height underestimates the differential delays by up to 0.3 ns under the same assumption. We believe these numbers would be even higher for higher solar activity conditions. An approximate value for the error we can expect by inappropriately setting the ionospheric shell height is about 0.5 TECU for every 50 km error in the height. This number corresponds to about 0.14 ns in the case of the differential delays. Also, these numbers could be different when modelling the ionosphere by fitting polynomials to the diurnal variation of TEC over a certain period of time. This procedure inherently averages over different ionospheric shell heights. This can also be a feasible explanation for our not detecting differences between the UNB and ESOC differential delay estimates.

CONCLUSIONS

The concept of accounting for the temporal and spatial variation of the ionospheric shell height using the IRI90 model has been described. We showed that on a small regional network of IGS stations, the predicted ionospheric shell height can vary with geographic location, time of day, season, and solar activity. After comparing our results with those obtained earlier using a fixed ionospheric shell height, we found differences in the differential delays of up to 0.3 ns. A similar study was conducted for the TEC estimates and we found that the estimates can be different by as much as 1 TECU when the temporal and spatial variation of the ionospheric shell height is not considered. We believe that these differences can be even larger during high solar activity conditions.

Furthermore, taking into account the temporal and spatial variation of the ionospheric shell height provides a more rigorous approach when estimating ionospheric model parameters along with satellite-receiver differential delays. By inappropriately setting the ionospheric shell height, we can expect a possible 0.5 TECU level error for every 50 km error in the shell height. For the differential delays, the equivalent error level is about 0.14 ns.

ACKNOWLEDGEMENTS

We greatly appreciate the assistance of Dieter Bilitza in providing us with an update of the IRI90 model. Funding from the University of New Brunswick and the Natural Sciences and Engineering Research Council of Canada is gratefully acknowledged. Without their help this research could not have been completed.

REFERENCES

Bilitza, D. (ed.) (1990). International Reference Ionosphere 1990. National Space Science Center/World Data Center A for Rockets and Satellites, Lanham, MD. Report Number NSSDC/WDC-A-R&S 90-22.

Bishop, G.J., A.J. Mazzella, and E.A. Holland (1995). "Application of Score Techniques to Improve Ionospheric Observations". ION GPS-95, Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation, Palm Springs, CA, 12-15 September, The Institute of Navigation, Alexandria, VA, pp. 1209-1218.

Coco, D.S., C.E. Coker, S.R. Dahlke, and J.R. Clynch (1991). "Variability of GPS Satellite Differential Group Delay Biases." IEEE Transactions on Aerospace Systems, Vol. 27, No. 6, pp. 931-938.

Coster, A.J., E.M. Gaposchkin, and L.E. Thornton (1992). "Real-time Ionospheric Monitoring System Using GPS." Navigation: Journal of the Institute of Navigation. Vol. 39, No. 2, pp. 191-204.

Davies, K. (1990). Ionospheric Radio. Peter Peregrinus Ltd., London, United Kingdom.

Freymueller, J. (1995). Personal communication. Department of Geophysics, Stanford University, Stanford, CA, January.

Gail, W.B., B. Prag, D.S. Coco, and C. Coker (1993). "A Statistical Characterization of Local Mid-latitude Total Electron Content." Journal of Geophysical Research, Vol. 98, No. A9, pp. 15,717-15,727.

Gao, Y., P. Heroux, and J. Kouba (1994). "Estimation of GPS Receiver and Satellite L1/L2 Signal Delay Biases Using Data from CACS." KIS94, Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics, and Navigation, Banff, Alberta, 30 August - 2 September, Department of Geomatics Engineering, The University of Calgary, Calgary, Alberta, pp. 109-117.

Hakegard, O.P. (1995). A Regional Ionospheric Model for Real-time Predictions of the Total Electron Content in Wide Area Differential Satellite Navigation Systems. Dr. Eng. Thesis, Norwegian Institute of Technology, Trondheim, Rapport 429506.

Klobuchar, J.A. (1986). "Design and Characteristics of the GPS Ionospheric Time Delay Algorithm for Single-Frequency Users." Proceedings of the PLANS-86 Conference, Las Vegas, NV, 4-7 November, pp. 280-286.

Komjathy, A., R.B. Langley, and F. Vejrazka (1995a). "A Comparison of Predicted and Measured Ionospheric Range Error Corrections." EOS Transactions of the American Geophysical Union, Vol. 76, No. 17, Spring Meeting Supplement, S87.

Komjathy, A., R.B. Langley, and F. Vejrazka (1995b). "Assessment of Two Methods to Provide Ionospheric Range Error Corrections for Single-frequency GPS Users." Presented at IUGG XXI General Assembly, Boulder, CO, 2-14 July 1995.

Komjathy, A. and R.B. Langley (1996). "An Assessment of Predicted and Measured Ionospheric Total Electron Content Using a Regional GPS Network." Presented at the ION National Technical Meeting, Santa Monica, CA, 22-24 January 1996.

Langley, R.B. (1996). "Propagation of the GPS Signals." in GPS for Geodesy, International School, Delft, The Netherlands, 26 March - 1 April, 1995. Springer-Verlag, New York.

Lanyi, G.E. and T. Roth (1988). "A Comparison of Mapped and Measured Total Ionospheric Electron Content Using Global Positioning System and Beacon Satellite Observations", Radio Science, Vol. 23, No. 4, pp. 483-492.

Mannucci, A., B. Wilson, and D. Yuan (1995). "An Improved Ionospheric Correction Method for Wide-Area Augmentation Systems." ION GPS-95, Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation, Palm Springs, CA, 12-15 September, The Institute of Navigation, Alexandria, VA, pp. 1199-1208.

National Geophysical Data Center, NGDC (1995). Geomagnetic Database, ftp://www.ngdc.noaa.gov/ STP/GEOMAGNET IC_DATA/INDICES/KP_AP/199.v12, accessed January 1996.

Newby, S.P. (1992). An Assessment of Empirical Models for the Prediction of the Transionospheric Propagation Delay of Radio Signals. M.Sc.E. thesis, Department of Surveying Engineering Technical Report No. 160, University of New Brunswick, Fredericton, N.B., Canada.

Runge, T., U. Lindqwister, A. Mannucci, M. Reyes, B. Wilson, and D. Yuan (1995). "Generation of GPS Observables for Global Ionospheric Mapping." EOS Transactions of the American Geophysical Union, Vol. 76, No. 17, Spring Meeting Supplement, S87.

Sardon, E., A. Rius, and N. Zarraoa (1994). "Estimation of the Transmitter and Receiver Differential Biases and the Ionospheric Total Electron Content from Global Positioning System Observations." Radio Science, Vol. 29, No. 3, pp. 577-586.

Schaer, S., G. Beutler, L. Mervart, and M. Rothacher (1995). "Global and Regional Ionosphere Models Using the GPS Double Difference Phase Observable." Presented at the 1995 IGS Workshop, Potsdam, Germany, 15-17 May.

Schwarz, K.P. (1987). "Kalman Filtering and Optimal Smoothing." Papers for the CISM Adjustment and Analysis Seminars, 2nd ed., The Canadian Institute of Surveying and Mapping, Ottawa, Ontario, Canada, pp. 230-264.

van der Wal, A. D. (1995). Evaluation of Strategies for Estimating Residual Neutral-atmosphere Propagation Delay in High Precision Global Positioning System Data Analysis. M.Sc.E thesis, Department of Geodesy and Geomatics Engineering Technical Report No. 177, University of New Brunswick, Fredericton, N.B., Canada.

Wilson, B. and A. Mannucci (1994). "Extracting Ionospheric Measurements from GPS in the Presence of Anti-spoofing." ION GPS-94, Proceedings of the 7th International Technical Meeting of the Satellite Division of The Institute of Navigation, Salt Lake City, UH, 20-23 September, The Institute of Navigation, Alexandria, VA, Vol. 2, pp. 1599-1608.

Return to Attila's Home Page

This page was compiled by Attila Komjathy and last updated 15 September 1997. If you have any questions, comments please feel free to get in touch with me.

You can reach me at: komjathy@ocean.colorado.edu